LAS TAREAS DE EVALUACIÓN IMPLEMENTADAS POR LOS FUTUROS DOCENTES DE MATEMÁTICA EN SUS PRÁCTICAS DIDÁCTICAS

ASSESSMENT TASKS IMPLEMENTED BY FUTURE MATHEMATICS TEACHERS IN THEIR DIDACTICS INTERNSHIPS

Ivana Marsicano

ivanamarsicano@gmail.com

Consejo de Formación de Educación, Uruguay

Recibido: 28 de julio de 2022

Aprobado: 21 de diciembre de 2022

Publicado: 1 de julio de 2023

Cita sugerida: Marsicano, I. (2023). Las tareas de evaluación implementadas por los futuros docentes de matemáticas en sus prácticas didácticas. Revista de la Escuela de Ciencias de la Educación. 2(18) 38-55.

RESUMEN

En este trabajo se analizan las características, según el tipo de tarea y la demanda cognitiva, de 171 actividades implementadas en las aulas de práctica didáctica de formación de 12 estudiantes de profesorado en matemática para la educación media en Uruguay. Los resultados muestran que las actividades de alta demanda cognitiva, que fueron diseñadas a partir de los lineamientos dados por la investigación en didáctica de la matemática para el diseño de tareas y que dialogan con los desafíos actuales de la evaluación de los aprendizajes en el aula, están escindidas de las que se utilizan para la certificación de saberes. Este hecho, puede llevar, no sólo a reducir la evaluación a la valoración y certificación de saberes, distinguiendo momentos para las inferencias formativas y sumativas con el tipo de actividades propuestas, sino que también a restringir las instancias y oportunidades para que los estudiantes sean partícipes activos, coconstruyan y se empoderen de su proceso de aprendizaje a través de la evaluación.

Los hallazgos de este trabajo responden a los primeros resultados obtenidos de una investigación en curso en el marco de una tesis doctoral en Ciencias de la Educación, llevada a cabo en la Facultad de Filosofía y Letras de la Universidad de Buenos Aires, cuyo propósito es estudiar las formas de pensar y actuar respecto a la evaluación de los aprendizajes de dos comunidades estrechamente vinculadas: los formadores de docentes en la rama de didáctica de la matemática y sus estudiantes que realizan prácticas preprofesionales de formación con grupos a cargo.

Palabras clave: Evaluación – Evaluación Matemática – Educación Matemática – Prácticas Didácticas – Formación Docente.

ABSTRACT

This paper analyses the characteristics, according to the type of task and cognitive demand, of 171 activities implemented in the didactic practice classrooms of 12 mathematics teacher training students for secondary education in Uruguay. The results show that the activities of high cognitive demand, which were designed based on the guidelines given by research in didactics of mathematics for the design of tasks and that dialogue with the current challenges of the assessment of learning in the classroom, are separated from those used for the certification of knowledge. This can lead not only to reducing assessment to the evaluation and certification of knowledge, distinguishing moments for formative and summative inferences with the type of activities proposed, but also to restricting the instances and opportunities for students to be active participants, to co-construct and empower themselves in their learning process through assessment.

The findings of this paper respond to the first results obtained from an ongoing research within the framework of a doctoral thesis in Educational Sciences, carried out at the Faculty of Philosophy and Arts of the University of Buenos Aires, whose purpose is to study the ways of thinking and acting with respect to the assessment of learning of two closely linked communities: teacher educators in the field of didactics of mathematics and their students who carry out pre-professional training practices with groups in charge.

Keywords: Assessment – Mathematics Assessment – Mathematics Education – Didactic Internships – Teacher Training.

INTRODUCCIÓN

Diferentes organizaciones internacionales que han desarrollado investigaciones y estudios sobre la formación y la práctica docente en matemática se han manifestado al respecto de las prácticas de enseñanza y de evaluación. La International Commission on Mathematical Intruction (ICMI) reporta un desajuste entre las metas y los logros de la educación matemática y los modos y formas de evaluación prevalentes en las aulas (Niss, 1993). Por su parte, la National Council of Teachers of Mathematics (NCTM) especifica que los profesores deben de tener más claridad al respecto de lo que se debe de enseñar y aprender de tal manera que la evaluación garantice que cada estudiante avance productivamente en la dirección apropiada y explicita que la evaluación debe de apoyar el aprendizaje de la matemática y proveer información útil tanto a docentes como a estudiantes (NCTM 1989, 1991, 2000).

Los retos actuales respecto a la evaluación de los aprendizajes en el aula se sustentan en tres puntos centrales relacionados: la participación de los estudiantes en todos los momentos del desarrollo de la evaluación, la retroalimentación efectiva y la implementación de tareas de calidad. Las tareas de calidad suponen un diseño que ofrezca la posibilidad de que los estudiantes se enfrenten a desafíos intelectuales retadores, de alto nivel intelectual, que les permitan tener un papel activo, que se propicie el diálogo y se pueda efectivizar una retroalimentación efectiva (Ibarra-Sáiz y Rodríguez-Gómez, 2020).

Para la educación matemática, el diseño y uso de las tareas es parte de su núcleo (Artiguey y Perrin-Glorian, 1991) y la implementación de una evaluación en el aula de matemática de carácter formativo promulga el uso de una gama de tareas no rutinarias que requieren que los estudiantes presenten información, hagan estimaciones prácticas, revisen y critiquen argumentos, evalúen y recomienden opciones, diseñen, planifiquen, definan conceptos, así como que muestren solvencia en los ejercicios técnicos (Burkhardt y Schoenfeld, 2019).

En el ámbito de formación docente, el diseño y la implementación de tareas son un medio técnico y conceptual que permite a los futuros docentes comprender y mejorar su práctica, es decir, son instrumentos que utilizan los formadores de docentes para que los futuros profesores desarrollen conocimiento y destrezas tanto para la enseñanza de la matemática, como para seguir aprendiendo en el ejercicio de la profesión (Llinares, 2011).

En el escenario de la formación docente y del aprendizaje en práctica, las residencias docentes (prácticas preprofesionales de formación, prácticas didácticas o pasantías) son instancias claves para el desarrollo profesional de un docente que dialogue con su práctica en el ejercicio de la profesión.

Este trabajo focaliza su atención en el centro de la formación práctica de los futuros profesores de matemática para la educación media y estudia las características de actividades implementadas por estos en sus grupos a cargo de la educación media correspondientes a la última práctica didáctica de formación y primera experiencia laboral en formación.

Los hallazgos de este trabajo responden a los primeros resultados obtenidos de una investigación en curso en el marco de una tesis doctoral, en Ciencias de la Educación, llevada a cabo en la Facultad de Filosofía y Letras de la Universidad de Buenos Aires, cuyo propósito es estudiar las formas de pensar y actuar respecto a la evaluación de los aprendizajes de dos comunidades estrechamente vinculadas: los formadores de docentes en la rama de didáctica de la matemática y sus estudiantes que realizan prácticas preprofesionales de formación con grupos a cargo.

DESARROLLO

Antecedentes sobre las formas prevalentes de evaluación en las aulas Desde la comunidad nacional, regional e internacional se reporta la importancia de entender que la evaluación de los aprendizajes no debe de asociarse únicamente a la certificación o a la medición de resultados y que, en la práctica de aula, de todos los niveles educativos, se suele confundir evaluación con calificación (Ravela et al., 2014; INEEd, 2015; Castro, Marsicano y Requena, 2019; Rajchman, 2019; Celman et al., 2009; López-Pastor y Pérez-Pueyo, 2017; Fraile, Pardo y Panadero, 2017).

Concretamente para el área de matemática, Giménez (1997) reporta que los profesores de la disciplina muestran una imagen tradicional y conservadora de la evaluación y que la práctica evaluativa reconoce hábitos tales como: la valoración casi única de los elementos conceptuales, una culpabilización del estudiante como único paciente de análisis y de fracaso, al docente como único agente evaluador, el examen como instrumento crucial y a la evaluación como acto de conclusión de un proceso y no como análisis de éste. Además, Giménez (1997) identifica varias dicotomías respecto a la evaluación, entre las que subraya las siguientes cuatro: entre la teoría y la práctica; entre el análisis sistémico de la evaluación y su consideración instrumental; entre la evaluación como juicio y la valoración como análisis comprensivo; entre la multiplicidad de fuentes de información, necesarias para que la valoración y juicio sobre el conocimiento de los estudiantes se haga sobre la mayor cantidad de datos y evidencia posible, y los estándares de calidad establecidos para los instrumentos singulares de evaluación, como son la fiabilidad y validez.

En el 2014 Ravela et al. realizaron un estudio sobre las propuestas de evaluación implementada en la educación media de Chile, Colombia, Perú y Uruguay. Este estudio, que tuvo carácter descriptivo, exploratorio y comparado, involucró a 76 docentes, 1824 estudiantes, 353 propuestas y 4359 tareas. Se realizaron entrevistas a todos los docentes, se estudió documentación y se aplicó un cuestionario a los estudiantes. Los autores indican que en Uruguay y Chile se enfatiza más la evaluación de saberes que en Colombia y Perú en donde el énfasis está puesto en aspectos actitudinales, de hábitos de orden, prolijidad, higiene, así como de autoestima de los estudiantes. Se indica que en Uruguay predominan las tareas de respuesta construida y que se le otorga especial importancia al esfuerzo de los estudiantes, que las calificaciones se asignan a partir de un concepto construido que se forma el docente de cada estudiante. Al respecto, se señala que la calificación es un elemento omnipresente en todos los países y que, si bien los docentes lo experimentan como una obligación administrativa, se utiliza como forma de motivar y “formar” (Ravela et al., 2014, p. 41). Respecto a las tareas de evaluación, los autores señalan que en todos los países estudiados el requerimiento es de bajo nivel cognitivo, de recordar y enunciar contenidos. En Uruguay, junto a las preguntas abiertas se presentan tareas que requieren procesos cognitivos un poco más complejos. Asimismo, se resalta que la falta de situaciones que requieran niveles de cognición más complejos hace que los espacios de feedback, para que los estudiantes reflexionen sobre sus procesos de aprendizajes, sean reducidos y se señala que las devoluciones se enfocan al análisis del error cometido por el estudiante.

Particularmente en la educación media en matemática uruguaya, Rajchman (2019) realizó un estudio mixto de triangulación por convergencia para conocer cómo evalúan los aprendizajes en matemática los docentes de 10 liceos públicos de Montevideo de barrios con distinta realidad sociocultural. Se reporta que los tres aspectos centrales que conforman la evaluación de los docentes participantes son: el esfuerzo que realizan los estudiantes, el trabajo en clase y la conducta. Además, se indica que este hallazgo es coherente con lo que opinan los estudiantes que indicaron que el factor más tenido en cuenta por sus docentes para calificarlos es el esfuerzo que ponen por aprender.

En el ámbito de formación docente, Celman et al. (2009) llevaron a cabo en Argentina un trabajo con el propósito de analizar las prácticas y su resignificación como parte de la formación de los futuros docentes, cuyo eje estuvo marcado por la problemática en el campo de la evaluación educativa al interior de las propuestas pedagógico-didácticas y curriculares. En este trabajo las autoras indican que los docentes participantes expresaron que no fueron formados académicamente para evaluar y reconocieron que tienen dificultades para pensar instancias, instrumentos y recursos de evaluación desde enfoques pedagógicos y didácticos que puedan sostener solvencia teórica y construcción en el terreno. Mencionan que reconocieron una gran fragmentación, no advertida ni concientizada, entre las prácticas de enseñanza y las de evaluación al interior de las aulas de los institutos de formación docente. Por último, las autoras advierten que hubo dificultades en la producción de narrativas de las experiencias educativas por parte de los docentes participantes que los identificara como sujetos que les permitiera el reconocimiento de lo que se aprende en la práctica, lo que las llevó a pensar que esa dificultad para escribir y comunicar el sentido de las acciones viene dado por “las marcas que dejó impresa en las subjetividades docentes, la lógica de la evaluación como acreditación o rendición de cuentas” (Celman et al., 2009, p. 20).

En Uruguay, se estudiaron las modalidades de evaluación de los aprendizajes de 9 docentes en el área de Ciencias Naturales -Biología, Química y Física- y las creencias sobre la evaluación de los aprendizajes de 65 estudiantes del Instituto de Profesores Artigas (IPA) a través de un estudio de casos mediante una metodología mixta de corte descriptivo y explicativo.

Los resultados de esta investigación mostraron que las creencias acerca de la evaluación de los aprendizajes de los estudiantes están construidas en base a la acreditación de saberes con el fin de obtener logros académicos y que esa visión “determina una actuación y actitud de adiestramiento del alumno frente al aprendizaje en desmedro del valor intrínseco de los contenidos, el gusto por los mismos y los procesos que por su intermedio es posible desencadenar” (Shablico, 2014, p.175). Se reporta, además, que la visión de los estudiantes coincide con las valoraciones y opiniones expresadas por algunos de los docentes, en especial los dedicados al abordaje disciplinar, que mostraron tener un sobre valor hacia las calificaciones con sentido utilitarista desvinculando la evaluación de los procesos de enseñanza y aprendizaje. En general se indica que la evaluación de los aprendizajes es considerada como un “agujero negro” por los docentes participantes y que los docentes de materias específicas:

Se inclinan hacia enfoques tradicionales de evaluación centrados en los contenidos disciplinares y a través de los cuales se esperan respuestas fijas, exactas y que cuantifican el conocimiento. Por su parte, los docentes de materias del tronco común de formación desarrollan en su mayoría acciones innovadoras en relación con las formas comprensivas y reflexivas en la evaluación de los aprendizajes (Shablico, 2014, p.175).

Concretamente en el escenario de las prácticas didácticas de formación docente, a nivel internacional, Moore (2003) reporta que a pesar del esfuerzo que realizan los docentes de didáctica para ayudar a sus estudiantes en formación a examinar y pensar sus prácticas contra la teoría, la realidad indica que las preocupaciones que responden a cuestiones generales del aula como la organización y gestión del tiempo son el centro de la experiencia en práctica de formación. Para la disciplina, matemática, Schwartz et al. (2018) estudiaron la naturaleza de 250 retroalimentaciones escritas dadas a los estudiantes de magisterio por los docentes de didáctica de tres universidades estadounidenses después de las observaciones de clase, e indicaron que un tercio de las retroalimentaciones estudiadas no incluían ningún aspecto específico de la disciplina, y que cuando lo incluían, varios eran generales o no estaban en consonancia con la didáctica de la matemática promovida en los cursos teóricos.

No se encontraron antecedentes que aborden específicamente la evaluación de los aprendizajes en las prácticas didácticas en matemática educativa para la formación docente en Uruguay.

Marco teórico conceptual Tareas Matemáticas

Los objetivos y perspectivas de la enseñanza de la matemática han ido cambiando con la evolución de la investigación en el área se ha pasado de una perspectiva centrada en los contenidos, a una que además de prestar atención a los contenidos, incluye atención a las prácticas de enseñanza que fomentan el razonamiento, la demostración, la conjetura, la representación, etc. (NCTM, 1989; NCR, 1989). En sintonía con lo anterior, los estándares del National Council of Teachers of Mathematics promulgan las tareas y propuestas que ofrezcan a los estudiantes: poner en juego conocimientos previos en nuevas situaciones; el aprendizaje de nuevo conocimiento y/o el ejercicio de simbolizar, demostrar, conjeturar, etc. (NCTM, 1989, 2000).

En ese contexto, desde la comunidad nacional, regional e internacional ha habido interés en el estudio y la descripción de tareas para la enseñanza de la matemática que construyan puentes entre la teoría y la práctica y ofrezcan un abanico de posibilidades promoviendo distinto tipo de alternativas.

La conceptualización de tarea dada por la Comisión Internacional de Instrucción Matemática (ICMI), que publicó un libro especialmente dedicado al diseño de las tareas (Margolinas, 2014), las designa como herramientas mediadoras entre la enseñanza y el aprendizaje de la disciplina e indica que el centro del diseño de las tareas está en trabajar en cómo se relacionan estas con el aprendizaje y cómo se utilizan en términos didácticos y pedagógicos. Explícitamente la ICMI refiere a que el término tarea es amplio e incluye: ejercicios repetitivos, construcción de objetos, ejemplificación de definiciones, resolución de problemas, realización de un experimento o una investigación.

Artiguey y Perrin-Glorian (1991) indican que el diseño y uso de tareas son las acciones que generan la actividad que brinda la oportunidad de encontrar conceptos, ideas y estrategias matemáticas, así como usar y desarrollar el pensamiento matemático y los modos de investigación.

Con respecto a la docencia, la ICMI señala que en ella se incluye la selección, modificación, diseño, secuenciación, instalación, observación y evaluación de tareas (Margolinas, 2014). Respecto a la clase de matemática, Guberman y Leikin (2013) refieren a que la calidad de estas viene determinada por las tareas que el docente implementa y la forma en que solicita que los estudiantes se acerquen a ellas.

Tareas de final abierto

Zaslavsky (1995) plantea la necesidad de generar tareas para el aprendizaje de la matemática que permitan ser abordadas desde varias puertas de entrada y caminos diferentes y que además generen motivación para el aprendizaje. La autora propone modificar las tareas estándares y habituales utilizadas para la enseñanza de la matemática, en tareas de final abierto, esto es, con múltiples respuestas correctas. Indica que con pequeños cambios en una consigna se pueden generar grandes diferencias y muestra tres formas de realizar estos cambios: omitiendo un dato, re-redactando la consigna y solicitando un ejemplo.

Las tareas de final abierto permiten que cada estudiante aborde el trabajo según sus conocimientos previos, de acuerdo con sus posibilidades y ofrecen oportunidad para que todos puedan obtener una respuesta correcta. Su implementación promueve la comunicación y discusión matemática, incentiva el uso de tecnología para visualizar en forma rápida determinados casos concretos, incentiva el trabajo en equipo y colaborativo empoderando a sus integrantes. Además, son motores naturales para que los estudiantes comparen sus razonamientos, justificaciones, compartan comunicación y discurso matemático. Zaslavsky (1995) indica que las tareas de final abierto posibilitan la adquisición de un rol creativo de situaciones de aprendizaje por parte de los docentes y una visión más humanista de la disciplina dado que dejan en evidencia que en matemática no siempre hay únicos caminos ni únicas respuestas correctas.

Viñetas Conceptuales

Las viñetas conceptuales (del inglés, concept cartoon) son un tipo de tarea diseñadas para el tratamiento de errores y de las concepciones alternativas de los estudiantes (Dolyenko, et al, 2018).

Keogh et al. (2008) indican que “las viñetas conceptuales son ilustraciones que con un estilo de dibujo animado presentan un rango de puntos de vista sobre la matemática involucrada en situaciones cotidianas” (p.7). El formato de este tipo de tarea les permite a los estudiantes tanto validar o rechazar lo expresado por los personajes, como exponer sus propios argumentos e ideas (Dolyenko et al, 2020).

Dolyenko et al. (2018) muestran que las viñetas conceptuales pueden ser diseñadas y constituirse además en una tarea de final abierto -en el sentido dado por Zaslavsky (1995)-. Los autores proponen incluir una burbuja en blanco para que el estudiante tenga la posibilidad de dar su opinión acerca del tópico involucrado y subrayan que el propósito de la burbuja en blanco es que los estudiantes comuniquen y argumenten y no que ofrezcan la resolución correcta. Al respecto, indican que se puede optar por proponer un tópico matemático en donde los distintos personajes dan su opinión acerca de la cuestión planteada incluyendo la respuesta correcta y que el resto de las opiniones ofrezcan la oportunidad de discutir e intercambiar al respecto de los errores y alternativas más frecuentes en los estudiantes.

Keogh et al. (2008) indican que las viñetas conceptuales les ofrecen a los estudiantes la posibilidad de exponer su opinión sin exponerse a un error propio dado de que siempre tienen la posibilidad de “culpar al personaje por defender tal idea” (p.10).

Requerimiento cognitivo de las tareas matemáticas

Smith y Stein (1998) proponen una clasificación de tareas matemáticas según el requerimiento cognitivo en los siguientes cuatro niveles: tareas de memorización; de procedimiento sin conexión; de procedimiento con conexión, y para hacer matemática.

Las tareas de memorización implican la reproducción exacta de lo trabajado y aprendido previamente, ya sea de fórmulas, reglas, hechos o definiciones. El requerimiento es declarativo, no hay aplicación de procedimientos ni conexión entre conceptos o significados subyacentes a los hechos, fórmulas o definiciones utilizadas, las preguntas son cerradas, con una única solución, sin interpretaciones ni ambigüedades (Smith y Stein, 1998).

Las tareas de procedimiento sin conexión requieren el uso de procedimientos específicos o evidentes a partir de lo trabajado previamente, a partir de la experiencia explícita. No hay conexión entre conceptos o significados que subyacen. Están enfocadas en producir respuestas cortas, no requieren desarrollar comprensión matemática, las explicaciones que se requieren se centran únicamente en describir el procedimiento específico utilizado (Smith y Stein, 1998). Las tareas de memorización y de procedimiento sin conexión, son las categorizadas de bajo requerimiento cognitivo o de nivel inferior.

Las tareas de procedimiento con conexión centran la atención de los estudiantes en el uso de procedimientos con el fin de desarrollar niveles profundos de comprensión de conceptos e ideas matemáticas. Requieren el uso de: procedimientos generales y amplios que tengan conexiones a las ideas conceptuales subyacentes involucradas; la representación de múltiples formas como diagramas visuales, manipulables, símbolos y situaciones problemáticas. En este tipo de tareas los estudiantes deben participar con ideas y procedimientos para finalizarlas con éxito, si bien los procedimientos son generales, estas tareas no se realizan sin pensar (Smith y Stein, 1998).

Las tareas de hacer matemática requieren un pensamiento complejo no algorítmico a través de un enfoque o camino no explícito ni sugerido. Los estudiantes para poder resolver este tipo de tareas deben acceder a conocimientos y experiencias relevantes y hacer uso adecuado de estos conocimientos y experiencias. Estas tareas requieren de exploración para la comprensión de la naturaleza de los conceptos, procedimientos o relaciones matemáticas. Los estudiantes deben de analizar la tarea y examinar el alance y limitaciones de esta. Este tipo de actividades implican realizar un esfuerzo cognitivo considerable que puede implicar cierto nivel de ansiedad debido a su naturaleza de no ser predecible su proceso de solución, exigen autocontrol o autorregulación de los propios procesos cognitivos (Smith y Stein, 1998). Las tareas de procedimiento con conexión y de hacer matemática son las que corresponden a altos niveles de complejidad cognitivo.

Evaluación de los aprendizajes en el aula

En 2014, Dylan Wiliam, uno de los referentes contemporáneos de la evaluación formativa, realiza una revisión de los debates predominantes sobre la conceptualización de este tipo de evaluación e indica que, si bien no hay una definición consensuada, es fundamental el rol de tres actores en su implementación: docente, par y estudiante. Además, refiere a la vigencia de lo planteado por Black y Wiliam (1998) al respecto de que la evaluación formativa debe usarse para proporcionar información tanto a los estudiantes como a los docentes sobre cómo mejorar el aprendizaje y la enseñanza, siendo el feedback el medio central para su puesta en práctica.

Subraya que una característica importante de la evaluación formativa es que la distinción entre la evaluación formativa y sumativa se basa en la función que realmente cumple la evidencia obtenida por la evaluación y no en el tipo de evaluación que genera la evidencia. En este sentido, Wiliam menciona que “describir una evaluación como formativa es cometer lo que Ryle (1949) describió como un error de categoría: atribuir a algo una propiedad que no puede tener” (p. 6). Al respecto, Cronbach (1971) remarca que una evaluación es un procedimiento para hacer inferencias y que son estas la que hacen la distinción: cuando las inferencias están relacionadas con las actividades de instrucción para maximizar el aprendizaje futuro, la evaluación funciona como formativa, y si las inferencias están relacionadas con el nivel de logro o los desempeños, entonces la evaluación es sumativa (Wiliam, 2014).

Lo anterior refuerza que la distinción sumativa-formativa se da en términos de los tipos de inferencia que están respaldadas por la evidencia obtenida por la evaluación y no por tipos de evaluaciones en sí, además, la misma evidencia puede respaldar ambos tipos de inferencias. Esta forma de entender la evaluación de los aprendizajes promulga un quehacer coherente con una práctica docente que integra la evaluación tanto para mejorar los procesos de enseñanza y aprendizaje como para certificar los saberes.

Ibarra-Sáiz y Rodríguez-Gómez (2020) indican que, en la última década, para el ámbito de la educación superior, el foco de atención respecto a la evaluación de los aprendizajes se centra en el aprendizaje estratégico de los estudiantes y el aprendizaje a lo largo de la vida; y refieren a la importancia de considerar la participación de los estudiantes; la retroalimentación efectiva, y la implementación de tareas de calidad en la práctica evaluativa. Indican que la participación de los estudiantes se puede establecer en tres momentos del proceso de evaluación: la planificación, el desarrollo y los resultados, y que esta refiere a favorecer el diálogo y la colaboración de los estudiantes fomentando instancias de autoevaluación, evaluación entre pares, coevaluación y evaluación compartida.

Vinculado a los instrumentos de evaluación que permiten la implementación de una evaluación formativa conjugando los procesos de certificación, Fraile, Pardo y Panadero (2017) reportan que las rúbricas, adecuadamente diseñadas e implementadas, facilitan tanto los procesos de calificación, como la implementación de una evaluación formativa y el desarrollo de la autorregulación del aprendizaje. Los aspectos más relevantes para la adecuada creación e implementación de rúbricas son: identificar los objetivos esenciales para definir los aspectos y niveles involucrados, así como el tipo de rúbrica a utilizar (Fraile, Pardo y Panadero, 2017); en los descriptores incorporar errores y puntos de destaque (Andrade, 2000); familiarizar a los estudiantes en su uso y al respecto se sugiere fuertemente la cocreación con los estudiantes de estos instrumentos (Fraile, Pardo y Panadero, 2017); utilizar las rúbricas en propuestas y actividades metacognitivas, así como incluir su uso en instancias de coevaluación y autoevaluación y en propuestas que permitan volver sobre lo realizado (Fraile, Pardo y Panadero, 2017).

Las escalas graduadas, consideradas por algunos autores como una evolución de las rúbricas, favorecen la implicación de los estudiantes en los procesos de evaluación y permiten mayores márgenes de precisión, presentándose como más adecuadas para producciones que impliquen componentes creativos de autor (López-Pastor et al., 2016; Pérez-Pueyo y Sobejano, 2017; Pérez-Pueyo et al., 2019). Esta reportado que los estudiantes valoran positivamente el uso y cocreación de las escalas graduadas señalando que su utilización y participación en la creación ofrece transparencia, facilita la elaboración del trabajo y calidad del logro (López-Pastor et al., 2016; Marsicano, 2019 y 2020).

Burkhardt y Schoenfeld (2019) indican que el desafío central de la evaluación formativa es que el docente desarrolle su experiencia y conciencia de las necesidades específicas del aprendizaje de los estudiantes y se adapte a ellas, tanto en la planificación, como en la orientación de la actividad momento a momento en el aula. Los autores señalan que la variedad de tareas de enseñanza es un tema central en el diseño del plan y de la evaluación ya que han comprobado que la especificación de la gama de tareas es la forma más clara de comunicar los objetivos de aprendizaje. Particularmente para matemática, indican que la gama de tareas a abordar debería contener una gran parte de problemas no rutinarios que soliciten a los estudiantes volver a presentar información, hacer estimaciones prácticas, revisar y criticar argumentos, evaluar y recomendar opciones, diseñar, planificar y definir conceptos, así como mostrar solvencia en los ejercicios técnicos.

Vinculado al tiempo de trabajo docente y a la limitante que implica a la hora de dar seguimiento individual a las respuestas de los estudiantes, Burkhardt y Schoenfeld (2019), sugieren centrar la atención en dos aspectos: en los típicos conceptos erróneos de los estudiantes reportados en la literatura para la temática y en el trabajo entre pares por parte de los estudiantes. Estos autores proponen considerar los siguientes aspectos para el diseño e implementación de una evaluación formativa en matemática:

1.- Basarse en los conocimientos que tienen los estudiantes, lo que implica adaptar la enseñanza a las necesidades del aprendizaje.

2.- Exponer y discutir conceptos erróneos comunes y otros sorprendentes, lo que implica que las actividades y tareas deben exponer el conocimiento actual y generar tensiones con éstos ofreciendo oportunidades de resolución.

3.- Utilizar preguntas de orden superior, esto significa preguntas que promuevan explicación, aplicación y síntesis.

4.- Utilizar adecuadamente la enseñanza interactiva, trabajo individual y cooperativo en pequeños grupos, esto implica propiciar el trabajo colaborativo después que los estudiantes hayan tenido oportunidad de reflexionar en forma individual, fomentar el debate crítico y constructivo en lugar de la discusión o aceptación acrítica.

5.- Crear conexiones entre los tópicos matemáticos abordados y los del entorno del mundo real.

6.- Fomentar el razonamiento más que la obtención de respuestas, así como la generación de conexiones y puentes entre los conceptos matemáticos abordados. 7.- Implementar tareas complejas y colaborativas, esto es tareas accesibles, ampliables, que fomenten la decisión y el hacer, el debate, la creatividad y el cuestionamiento.

8.- Afrontar y adelantarse a las dificultades en lugar de evitarlas, esto significa, plantear una enseñanza que desafía a los alumnos y tiene expectativas sobre ellos. No se trata de un rol de “allanar caminos” sino de generar situaciones y dificultades realistas a superar.

9.- Desarrollar el lenguaje matemático a través de actividades comunicativas tanto orales como escritas.

10.- Reflexionar sobre el aprendizaje que ha tenido lugar.

11.- Utilizar los recursos tecnológicos en forma apropiada y creativa.

Metodología

Con el objetivo de estudiar las características de las evaluaciones implementadas por los estudiantes de profesorado en matemática para la educación media en Uruguay, en el contexto de sus últimas prácticas didácticas preprofesionales de formación de la carrera docente, en este trabajo se analizan las características de 171 actividades propuestas por 12 estudiantes que conforman la muestra de este estudio.

Los 12 estudiantes corresponden a la totalidad de estudiantes que realizaron en 2019 el curso de Didáctica III en el Instituto de Profesores Artigas (único instituto de formación docente público de Montevideo) y de los Centros Regionales de Docentes del Sur y Suroeste de Uruguay.

El curso de Didáctica III de la carrera de profesorado en matemática es un curso teórico-práctico con un docente de didáctica a cargo tanto de la parte teórica -en el instituto de formación correspondiente-como de la parte práctica con el rol de docente de práctica.

Las actividades analizadas en este trabajo fueron suministradas por los estudiantes junto a la planificación anual del curso y de las clases en donde fueron visitados por sus docentes de Didáctica III. Todos los insumos fueron suministrados por los estudiantes cuyo contacto se realizó por medio de correo electrónico.

Las 171 actividades analizadas corresponden tanto a secuencias implementadas por los estudiantes en las clases que fueron visitados por sus docentes de Didáctica III, como a evaluaciones escritas propuestas para la certificación de saberes.

El análisis sobre las características de las 171 actividades se realizó tanto estudiando su requerimiento cognitivo, a partir de la categorización dada por Smith y Stein (1998) para las actividades matemáticas: de memorización, de procedimiento sin conexión, de procedimiento con conexión y de hacer matemática; como considerando sus particularidades respecto a las características que presentan las tareas de final abierto (Zaslavsky, 1995 y 2008) y las viñetas conceptuales (Dolyenko et al., 2020).

En el caso de las actividades propuestas en clase, se consideró si en las planificaciones se previeron instancias de feedback, evaluación entre pares, coevaluación y/o autoevaluación. También si se proyectó la utilización de rúbricas y si estas actividades recibieron valoración para la certificación de saberes.

CONCLUSIONES

El estudio sobre la demanda cognitiva de las actividades analizadas muestra que 154 fueron de demanda cognitiva baja englobando las actividades de memorización y de procedimiento sin conexión y 17 de demanda cognitiva alta englobando las actividades de procedimiento con conexión y de hacer matemática.

En la siguiente Tabla 1 se ilustran los resultados obtenidos respecto a la demanda cognitiva de las 171 actividades analizadas desglosadas según cada uno de los niveles.

Tabla 1

Demanda cognitiva de las actividades

	Memorización	Procedimiento Sin Conexión	Procedimiento Con Conexión	Hacer Matemática
Demanda Cognitiva	Baja		Alta
Cantidad	25	129	14	3

De esas 154 actividades de demanda cognitiva baja, 25 están en el nivel de memorización y 129 en el de procedimiento sin conexión.

Las 25 actividades de memorización conforman evaluaciones para la certificación de saberes propuestas en escritos en clase de realización individual. Para las actividades de procedimiento sin conexión, 124 son las que conforman evaluaciones para la certificación de saberes propuestas en escritos en clase de realización individual.

En la siguiente Figura 1 se ilustra una actividad de requerimiento cognitivo bajo, categorizada de procedimiento sin conexión, que fue utilizada en una evaluación escrita para la certificación de saberes y propuesta en tercer año de liceo del ciclo básico, estudiantes de 14-15 años. Su resolución requiere, primeramente, identificar del par ordenado dado el valor correspondiente a cada una de las variables, luego sustitiur cada uno de los valores en las ecuaciones dadas y realizar los cálculos correspondientes entre los números enteros involucrados. Estos cálcuos involucran multiplicaciónes, sumas y restas que permiten comrpobar si se verifican las igualdades planteadas.

Respecto a las actividades de demanda cognitiva alta, de las 17 analizadas, que involucran tanto las actividades de procedimiento con conexión como las de de hacer matemática, 14 se enmarcan en el tipo de tareas de final abierto. De esas 14 actividades, 4 tienen formato de viñetas conceptuales.

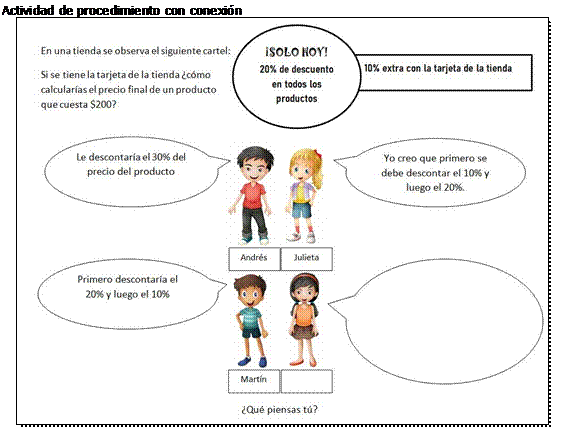
En la Figura 2 se ilustra una actividad de requerimiento cognitivo alto, categorizada como de procedimiento con conexión, con formato de viñeta conceptual abierta -propuesta en primer año de liceo del ciclo básico, estudiantes de 12-13 años- que fue implementada en clase para trabajar sobre los porcentajes de descuentos acumulados que suelen ofrecerse en las promociones comerciales. Si bien en esta actividad se fija un monto, precio, su resolución requiere que los estudiantes reflexionen sobre los procedimientos involucrados posibilitando la generalización y habilitando niveles más profundos de comprensión de los conceptos e ideas matemáticas que subyacen a los procedimientos.

Figura 2

De las 129 actividades de procedimiento sin conexión analizadas, 5 corresponden a propuestas trabajadas en clases, involucrando 5 planificaciones de clase para su implementación. Por otra parte, las 17 actividades de demanda cognitiva alta corresponden a secuencias de clase que involucran 8 planificaciones. Ninguna de las actividades de alta demanda cognitiva fue utilizada para la certificación de saberes.

En ninguna de las planificaciones estudiadas se proyectan instancias de peer feedback, feedback, coevaluación y/o autoevaluación, ni de utilización de rúbricas y/o escalas graduadas.

En todas se realiza un análisis a priori de las actividades y se proyecta la implementación bajo un esquema de clase que involucra una puesta en común y una institucionalización de los resultados, procedimientos y conceptos involucrados. Los objetivos plasmados mayoritariamente son temáticos/conceptuales y no se explicitan expectativas de logro para los aprendizajes.

Tanto en el análisis a priori de las actividades como en la proyección de la puesta en común e institucionalización, se formulan una serie de preguntas con el fin de fomentar la respuesta de los estudiantes y el diálogo docente-estudiante. A excepción de una de las planificaciones, la implementación de las actividades se proyecta para ser resueltas en forma individual o con el compañero sentado al lado, y en este último caso, sin una planeación específica respecto a la dinámica de trabajo de a pares.

En una de las planificaciones, que involucra una actividad de alta demanda cognitiva, se explicitan una serie de preguntas para dinamizar el diálogo estudiante-estudiante durante una dinámica de trabajo grupal y se indica que se tomará nota de las estrategias tomadas por los estudiantes para luego “retomarlas en la conversación y construcción de la puesta en común y la institucionalización”.

Discusiones

En este trabajo, las actividades estudiadas de bajo requerimiento cognitivo, clasificadas como de memorización y de procedimiento sin conexión (Smith y Stein, 1998), son cerradas y se centran en que los estudiantes puedan identificar, reproducir y/o aplicar procedimientos específicos o algorítmicos. Estas características restringen, tanto la generación de un diálogo rico y conceptual de los objetos matemáticos involucrados como las posibilidades de implementar feedback y peer feedback más allá de los resultados obtenidos y/o de los procedimientos específicos involucrados.

Las actividades de alta demanda cognitiva estudiadas, clasificadas como de procedimiento con conexión y de hacer matemática (Smith y Stein, 1998), en su gran mayoría fueron diseñadas siguiendo la evidencia ofrecida por la didáctica de la matemática para el diseño de tareas posibilitando, entre otras cosas, un diálogo rico y que todos los estudiantes sean partícipes activos en la construcción de su conocimiento a partir de sus saberes previos (Zaslavky, 1995; Dolyenko et al, 2020). Estas actividades fueron implementadas en forma independiente a las que se implementaron para la certificación de saberes y, al igual que las de baja demanda cognitiva, no previeron la inclusión de espacios de coevaluación y autoevaluación, ni un trabajo con instrumentos como rúbricas y/o escalas graduadas, que son vehículos tanto para la participación real de los estudiantes en todos los procesos de evaluación, como para conjugar la implementación de una evaluación formativa con la certificación de saberes (Fraile, Prado y Panadero, 2017; Marsicano, 2019 y 2020).

Esto significa que, en este estudio, las actividades de alta demanda cognitiva, que dialogan con un diseño de tareas fundamentado en la investigación didáctica de la disciplina y que propician el diálogo y la retroalimentación efectiva, fueron implementadas de manera independiente de las que fueron utilizadas para la certificación de saberes que presentan características limitadas para hacer inferencias formativas. Este hecho, puede llevar no sólo a reducir la evaluación a la valoración y certificación de saberes, distinguiendo momentos para las inferencias formativas y sumativas con el tipo de actividades propuestas, sino que también restringe las instancias y oportunidades para que los estudiantes sean partícipes activos, coconstruyan y se empoderen de su proceso de aprendizaje a través de la evaluación.

Al respecto de las actividades que ofrecen mayores oportunidades para hacer inferencias formativas, en este estudio, de las 171 actividades estudiadas, menos del 10% corresponden a tareas de alta demanda cognitiva realizadas siguiendo la acumulación de conocimiento ofrecida desde la didáctica de la disciplina para el diseño de tareas. Por otro lado, pero enlazado con este hecho, a excepción de una de las planificaciones estudiadas en este trabajo, en ninguna se explicita la organización de un trabajo cooperativo y colaborativo entre los estudiantes y la proyección de un diálogo estudiante-estudiante. Este hecho, junto al desbalance en la demanda cognitiva de las tareas implementadas, la falta de instancias planificadas de feedback, peer feedback, coevaluación, autoevaluación, uso y coconstrucción de rúbricas y escalas graduadas, minimizan tanto las oportunidades de diálogo e interacción dadas por la naturaleza del diseño de las actividades como la posibilidad de que los estudiantes puedan volver sobre lo realizado e inferir de una misma actividad insumos formativos como sumativos.

Estas conclusiones, si bien adolecen de un poder generalizador, tanto por las características de la muestra como por las limitaciones dadas por el análisis exclusivo de fuentes documentales (planificaciones, secuencias didácticas, escritos), sus resultados muestran la relevancia y necesidad de seguir investigando y obteniendo insumos sobre las prácticas de evaluación didáctica implementadas en las aulas.

Agradecimiento

Este artículo ha sido posible gracias a la financiación del Ministerio de Educación y Cultura de Uruguay en el marco de las becas de posgrado Carlos Quijano.

REFERENCIAS

Artiguey, M. y Perrin-Glorian, M.J. (1991). Didactic engineering, research, and development tool: some theoretical problems linked to this duality. For the learning of

Mathematics 11(1), 3-17.

Black, P. y Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education, 5, pp. 7-74

Burkhardt, H. y Schoenfeld, A. (2019). Formative Assessment in Mathematics, in Handbook of Formative Assessment in the Disciplines. Routledge

Castro, S., Marsicano, I. y Requena, G. (2019). Evaluación formativa en matemática: una experiencia en el primer año de la educación media básica. Informes ANII.

https://www.anii.org.uy/upcms/files/listadodocumentos/documentos/fondo-sectorial-educaci-n.pdf

Celman, S.; Galarraga, G., Rafaghelli, M., Martínez, M., Grinóvero, N., Gerard, A. y Osella, J. (2009). Aportes de la evaluación para la formación docente.

Itinerarios Educativos, 3(3), 1-15. doi: https://doi.org/10.14409/ie.v1i3.3911

Cronbach, L. J. (1971). Test validation. In R. L. Thorndike (Ed.), Educational measurement (2 ed., pp. 443-507). American Council on Education.

Dolyenko, L.; González, D.; Gonzáles, L. y Ochoviet, C. (2018). Las viñetas conceptuales en el aula de Matemática: Un recurso potente para enseñar y para aprender. En

Molfino, V. Ochoviet, C. (Eds.), Estrechando lazos entre investigación y formación en Matemática educativa: Experiencias conjuntas de docentes y futuros docentes.

5(43-66). Consejo de Formación en Educación.

Fraile, J.; Pardo, R. y Panadero, E. (2017). ¿Cómo emplear las rúbricas para implementar una verdadera evaluación formativa? Revista Complutense de Educación, 28 (4),

1321-1334.

Giménez, J. (1997). Evaluación en matemática: una integración de perspectivas. Síntesis Editorial.

Guberman, R. y Leikin R. (2013). Interesting and difficult mathematical problems: charing teacher´s views by employing multiple-solutuion task. Journal of Mathematics Teacher Education, 16, 33-56.

Ibarra-Sáiz, M. y Rodríguez-Gómez, G. (2020). Aprendiendo a evaluar para aprender en la Educación Superior. Revista Iberoamericana de Evaluación Educativa, 13(1), 5–8.

Instituto Nacional de Evaluación Educativa (INEEd). (2015). Evaluación y tránsito educativo. INEEd.

Keogh, B., Dabell, J. y Naylor, S. (2008). Concept Cartoons in Mathematics Education. Millgate House Publishers.

Llinares, S. (2011). Tareas matemáticas en la formación de maestros. Caracterizando perspectivas. Números. Revista de Didáctica de las Matemáticas, 79, 5-16.

López-Pastor, V. y Pérez-Pueyo, A. (2017). Evaluación formativa y compartida en educación: experiencias de éxito en todas las etapas educativas. Universidad de León. https://buleria.unileon.es/handle/10612/5999 López-Pastor, V.; Pérez-Pueyo, Á.; Barba, J. y Lorente-Catalán, E. (2016). Percepción del alumnado sobre la utilización de una escala graduada para la autoevaluación y coevaluación de trabajos escritos en la formación inicial del profesorado de educación física (FIPEF). Cultura, Ciencia y Deporte, 11(31), 37–50.

Margolinas, C. (2014). Task Design in Mathematics Education. Proceedings of ICMI Study 22. ICMI Study, Oxford, United Kingdom.

Marsicano, I. (2020). Escalas graduadas cocreadas: una experiencia en la educación remota de emergencia. Reloj De Agua, (22).

Marsicano, I. (2019). Utilización de escalas graduadas para autoevaluar y coevaluar: una experiencia de aula en la educación virtual superior. Infancia, Educación y

Aprendizaje (IEYA), 5(2), 143–147. doi:10.22370/ieya.2019.5.2.1690

Moore, R. (2003). Reexamining The Field Experiences Of Preservice Teachers. Journal of Teacher Education, 54(1), 31–42. doi: https://doi.org/10.1177/0022487102238656

National Research Council (1989). Everybody counts: a report to the nation on the future of mathematics education. National Academic Press.

National Council of Teachers of Mathematics (1989). Curriculum and Evaluation Standards for School Mathematics. National Council of Teachers of Mathematics.

National Council of Teachers of Mathematics (1991). Professional Standards for Teaching Mathematics. National Council of Teachers of Mathematics.

National Council of Teachers of Mathematics (2000). Principles and Standards for School Mathematics. National Council of Teachers of Mathematics.

Niss, M. (1993). Investigations into Assessment in Mathematics Education - An ICMI Study, Kluwer Academic Publishers.

Pérez-Pueyo, Á. y Sobejano, M. (2017). Elaboración de instrumentos (escalas de valoración y graduadas) para la evaluación formativa. Revista Infancia, Educación y

Aprendizaje, 3(2), 808–814.

Pérez-Pueyo, Á.; Hortigüela-Alcalá, D. y Gutiérrez-García, C. (2019). La evaluación del alumnado: tan cotidiana y, sin embargo, tan mejorable. La necesidad de nuevos

instrumentos. Cuadernos de Pedagogía. Evaluar para Aprender, 504, 54–63.

Rajchman Goldfarb, A. (2019). ¿Cómo se evalúan los aprendizajes de Matemática en Educación Secundaria según las perspectivas de docentes y estudiantes en 10

liceos de Montevideo?: un estudio mixto de triangulación por convergencia. [Tesis de Maestría]. Universidad ORT Uruguay, Instituto de Educación. Recuperado de

https://dspace.ort.edu.uy/handle/20.500.11968/4018

Ravela, P.; Leymonié, J.; Viñas, J. y Haretche, C. (2014). La evaluación en las aulas de secundaria básica en cuatro países de América Latina. Propuesta Educativa, 41(1), 20-

45

Schwartz, C.; Walkowiak, T. A., Poling, L., Richardson, K. y Polly, D. (2018). The nature of feedback given to elementary student teachers from university supervisors after

observations of mathematics lessons. Mathematics Teacher Education & Development, 1(20), 62-85.

Shablico, D. (2014). La evaluación de los aprendizajes: un análisis sobre las modalidades aplicadas en la formación de profesores del Instituto de Profesores Artigas. Cuadernos

de Investigación Educativa. 5(20). Universidad ORT Uruguay.

Smith, M. y Stein, M. (1998). Selecting and Creating Mathematical Tasks: From Research to Practice. Mathematics Teaching in the Middle School (3), 5, 344-350.

Wiliam, D. (2014). Formative assessment and contingency in the regulation of learning processes. Symposium entitled Toward a Theory of Classroom Assessment as the

Regulation of Learning at the annual meeting of the American Educational Research Association.

Zaslavsky, O. (1995). Open-ended tasks as a trigger for mathematics teachers’ professional development. For the Learning of Mathematics, 15(3), 15-20.

Zaslavsky, O. (2008). Attention to similarities and differences: A fundamental principle for task design and implementation in mathematics education.

Invited presentation at the Topic Study Group (TSG34) on Research and Development on Task Design and Analysis, the 11th International Congress on Mathematics Education (ICME-11).