LA
TECNOLOGÍA EN EVENTOS CONTEXTUALIZADOS PARA LA CONSTRUCCIÓN DEL CONOCIMIENTO DE
NÚMEROS COMPLEJOS EN INGENIERÍA
Christophe Mbe Koua
Ndjatchi*
UPIIZ, Instituto
Politécnico Nacional, México
Recibido: 23/09/2018
Aceptado: 30/11/2018
Resumen
La investigación tuvo como objetivo determinar
cómo favorece la tecnología en eventos contextualizados la construcción del
conocimiento de números complejos en los alumnos. Este trabajo se fundamentó en
la teoría de la
Matemática en el Contexto de las Ciencias (MCC). Los resultados mostraron que
la didáctica de la Matemática en Contexto contribuye a que los alumnos construyan
su conocimiento. Esto es, los alumnos de
Ingeniería en Sistemas Computacionales construyen su conocimiento de los
números complejos cuando la matemática se vincula con el objeto principal de
estudio de su carrera, dado que ellos tuvieron que desarrollar, en un lenguaje
de programación de alto nivel, una calculadora para números complejos.
Palabras
clave: Matemática
en el Contexto de las Ciencias – Matemática en Contexto – Proceso Cognitivo –
Eventos contextualizados – Números complejos.
Abstract
The purpose of this research is to determine how technology in
contextualized events, helps students to construct their knowledge of complex
numbers. This work is based on the theory of Mathematics in the Context of
Sciences (MCS). The results showed that the didactic of mathematics in context,
helps students to construct their knowledge. Thus, computer systems engineering
students construct their knowledge on complex numbers when mathematics is
related to the study’s main aim of students’ career, since students were asked
to develop a calculator for complex numbers in high-level programming language.
Keywords: Mathematics in the Context of Sciences – Mathematics in Context –
Cognitive Process – Contextualized event – Complex numbers.
Introducción
Las ingenierías se caracterizan por fundamentarse en las
ciencias básicas. Para el caso de la matemática, las asignaturas anteriores a
las Matemáticas Avanzadas para la Ingeniería contienen temas que giran
alrededor de los números reales, mientras que las Matemáticas Avanzadas dan
inicio al estudio de un conjunto de números más amplio: el conjunto de los
números complejos.
Es importante mencionar que los números complejos, además de que
son usados en la ingeniería para entender problemas de asignaturas básicas como
la descripción de señales periódicas variables, también son empleados en
asignaturas subsecuentes de especialidad;
como el caso de la Ingeniería en Sistemas Computacionales (ISC), que se emplean en Electrónica Analógica y Teoría de Comunicaciones
y Señales, es decir, el tema de los números complejos es esencial para la ISC.
Por otro lado, el personal docente de la academia de
Físico-matemática de la profesión de la ISC, así como el Departamento de
Gestión Escolar de la Unidad Profesional Interdisciplinaria de Ingeniería de
Zacatecas del Instituto Politécnico Nacional (UPIIZ-IPN), han constatado un índice de reprobación muy alto (más del 60 por
ciento de los alumnos) en la asignatura que incorpora el tema de los números
complejos (Departamento de Gestión Escolar
UPIIZ-IPN, s.f.). Aunque la reprobación es sólo un síntoma,
la problemática es la falta de construcción del conocimiento de los números
complejos (Camarena 1984).
En
las últimas décadas, muchos investigadores del área de la didáctica de la
matemática se han dedicado a estudiar el impacto del método tradicional de
enseñanza de las matemáticas sobre el proceso de enseñanza y aprendizaje de las
matemáticas en las ingenierías. Camarena (2015) comenta que este método genera
una desvinculación entre la matemática y las demás materias de especialidad de
la profesión de ingeniería, provocando el desinterés de los alumnos.
Por esta razón, es importante buscar otra forma de enseñanza y
aprendizaje de los números complejos donde los alumnos construyan su
conocimiento. A
nivel mundial se han propuesto diferentes teorías para la didáctica de las
matemáticas, como la ingeniería didáctica de Brousseau (2002, 2008), la teoría educativa de la
Matemática en el Contexto de las Ciencias de Camarena
(1984, 2015),
entre otras.
La
teoría de la Matemática en el Contexto de las Ciencias (MCC) nace para las
ingenierías, ésta permite vincular la matemática con las demás asignaturas de
la profesión (Camarena, 1984, 2015; Ruiz, 2014). Este hecho ayuda al ingeniero a utilizar el conocimiento de las ciencias y la experiencia para encontrar los
mejores resultados de los problemas que enfrenta durante su labor profesional;
ya que él crea, durante este proceso de construcción de soluciones, diferentes
modelos matemáticos que le permiten analizar las situaciones rigurosamente y
probar sus resultados potenciales.
Por otro lado, en la
actualidad, la tecnología electrónica está presente en todos los ámbitos de la
educación, está puede ser considerada como un medio de trabajo en las diversas áreas institucionales, como un
objeto de estudio, como un medio de comunicación, como un ambiente de
aprendizaje, como un material de apoyo didáctico en los procesos de enseñanza y
de aprendizaje de los educandos (Camarena, 2014); en la mayoría de los casos, éstas
se utilizan cuando ya existen y el profesor las toma y emplea en su práctica
docente. Todo ello lleva a preguntarse si existe otro papel diferente a
lo conocido que pueda tomar la tecnología, con el fin de favorecer la
construcción del conocimiento del estudiante.
Tomando
en cuenta que la teoría de la MCC establece la vinculación de la matemática con
la profesión en estudio y que el objeto de estudio de las ingenierías
relacionadas con la tecnología electrónica es el desarrollo de software o
hardware, en particular para la profesión de ISC de la UPIIZ-IPN se busca, en
esta investigación, cómo incorporar la tecnología al proceso de enseñanza y de
aprendizaje de los números complejos con la teoría de la Matemática en el
Contexto de las Ciencias. Así, el objetivo de investigación es determinar cómo favorece la tecnología con la
teoría de la MCC la construcción del conocimiento de números complejos en los
alumnos.
Marco
teórico
La Matemática en el Contexto de las Ciencias,
teoría desarrollada por Camarena (1984, 1990, 2000, 2014, 2015), es una de las
teorías de enseñanza y aprendizaje de las matemáticas en la ingeniería, más
utilizada en México en las últimas décadas. Esta teoría tiene un carácter
social ya que se trata de analizar la matemática que será de utilidad a la
sociedad científica y técnica. Además, ésta trata de desarrollar una cultura
matemática entre sus usuarios y busca preparar al futuro profesionista a que
enfrente exitosamente su labor profesional (Camarena, 1984, 2014, 2015).
La MCC nació en 1982 en el Instituto
Politécnico Nacional (IPN) de México; ésta reflexiona sobre la relación que
debe existir entre la matemática y las demás ciencias que la requieran, con las
futuras actividades profesionales y laborales del alumno, así como con
situaciones de la vida cotidiana (Camarena, 1984, 1990, 2000, 2015).
Camarena (1984, 2015) recalca que la MCC aborda
cinco fases mediante un propósito en común de los saberes transdisciplinarios,
de tal forma que en el ambiente de aprendizaje están presentes las cinco fases
de la teoría: la curricular, desarrollada desde 1982, la
didáctica, iniciada desde 1987, la epistemológica, abordada en 1988, la
docente, definida en 1990, y la cognitiva, estudiada desde 1992.
La fase curricular contiene un proceso
metodológico para diseñar programas de estudio de las ciencias básicas en
profesiones donde estas ciencias no son una meta por sí mismas, esta
metodología se denomina DIPCING (Camarena, 2002).
A través de la fase didáctica de esta teoría,
se cuenta con la estrategia didáctica de la Matemática en Contexto (MC); la
cual parte de la estructura curricular y las competencias requeridas en el
campo profesional y laboral del futuro egresado, incursionando en la
vinculación entre disciplinas con el objetivo de ofrecer una formación de
integral al estudiante, donde los dos ejes rectores de la didáctica son la
contextualización y la descontextualización (Camarena, 1984, 2014).
Camarena (2000, 2002, 2015) contempla nueve
etapas en la estrategia didáctica: 1. identificación de los eventos
contextualizados, 2. planteamiento a los
equipos del evento contextualizado, 3. determinación de las variables y las
constantes del evento por los equipos, 4. inclusión de los temas y conceptos
matemáticos y del contexto, necesarios para el desarrollo del modelo matemático
y solución del evento, 5. determinación del modelo matemático por los equipos,
6. hallazgo de la solución matemática del evento por los
equipos, 7 . Determinación de la solución requerida por
el evento por
los equipos, 8. interpretación de la solución en términos
del evento, y 9. presentación de una matemática descontextualizada.
La didáctica de la MC se desarrolla en el
ambiente de aprendizaje a través de eventos contextualizados (event-cont), éstos pueden ser problemas,
proyectos o estudios de caso que se contextualizan en tres fuentes: temas de
las ciencias en estudio, actividades profesionales y laborales, así como
situaciones de la vida cotidiana.
Metodología
La
investigación es cuasi-experimental. Se forman dos grupos para ser comparados:
el grupo control y el grupo experimental.
La
metodología de trabajo incluye las nueve etapas de la didáctica de la
Matemática en Contexto; para lo cual la teoría de la MCC establece la necesidad
de saber con qué conocimientos previos del tema en estudio cuenta el estudiante
(Camarena, 1984; Ausubel, 1968); además, es
importante esta información para tener controlada esta variable en los dos grupos
de estudiantes de la investigación.
Para
la parte correspondiente a los conocimientos previos sobre los números
complejos, se tiene una investigación previa, donde se usaron los dos grupos
designados y Autor (2018) diseñó un instrumento para evaluar el conocimiento
previo de los estudiantes, de acuerdo a los procesos cognitivos que determinan
la construcción del conocimiento matemático propios de la teoría de la MCC,
mostrados en la tabla 1. El autor les aplicó
dicho instrumento y los resultados mostraron que ambos grupos tienen el mismo
tipo de deficiencias y aciertos en los prerrequisitos matemáticos indispensables para los números complejos.
Tabla 1. Procesos Cognitivos que determinan la construcción
del conocimiento de las ciencias básicas
|
Proceso Cognitivo |
Descripción del Proceso
Cognitivo |
|
ProCog 1 |
Construcción conceptual de temas y conceptos de cada disciplina
involucrada. Entre los aspectos que identifican este proceso están los
conocimientos previos, el tránsito entre registros semióticos y el tránsito
entre el lenguaje natural y el matemático y viceversa. |
|
ProCog 2 |
La operatividad de cada disciplina. Referiéndose a operaciones
mecánicas. |
|
ProCog 3 |
Un manejo o ejecución de procedimientos, técnicas y métodos de cada
disciplina. |
|
ProCog 4 |
La contextualización, en donde el estudiante identifica los contenidos
disciplinares que intervienen en un evento dado y las conexiones entre estos
contenidos. |
Fuente:
Flores y Camarena (2012)
Método de trabajo
De los dos grupos formados, el grupo control
recibe una clase tradicional, por su lado el grupo experimental toma una clase
contextualizada de dicho tema con base en la estrategia didáctica de la MC.
El método de trabajo consta de tres etapas:
(1) Construcción del evento contextualizado.
Con el fin de determinar la forma en que se
puedan vincular estos números con los conocimientos que tienen los estudiantes
sobre su profesión en estudio, la tecnología, se aplica la metodología Dipcing para vincular
la tecnología en event-cont.
(2)
Didáctica de la MC.
Se implementa, en el grupo experimental, la
estrategia didáctica de la MC para la construcción del conocimiento de los
números complejos en el contexto de la ISC.
(3)
Nivel de aprendizaje.
Se examina el nivel de aprendizaje que alcanzan
los estudiantes del grupo experimental con respecto a los estudiantes del grupo
control, al construir sus conocimientos en este tema cuando se emplea la MC.
Técnicas de investigación
Para la primera etapa se emplea el análisis de
textos que establece la metodología Dipcing en su etapa central, con lo cual se
identifican o construyen los event-cont que se aplican con la estrategia
didáctica de la MC y se verifica su validez.
Para aplicar, en el grupo experimental, la
estrategia didáctica de la MC propia de la teoría MCC, correspondiente a la
segunda etapa del método de trabajo, se aplican las nueve etapas de la
estrategia didáctica de la teoría de la MCC.
Para determinar el nivel alcanzado de
aprendizaje del estudiante al construir su conocimiento en este tema, es decir
para la tercera etapa del método de trabajo, se diseña un instrumento de
evaluación de acuerdo a los procesos cognitivos que determinan la construcción
del conocimiento matemático de la tabla 1, con ello se diseña una rúbrica que
determina los niveles de aprendizaje. Este instrumento se aplica a ambos grupos
de la experimentación.
La muestra
Se toma como muestra de estudio a dos grupos de
15 estudiantes cada uno de la carrera de ISC del cuarto semestre de la
UPIIZ-IPN. Cabe mencionar que la selección de la muestra es no probabilística,
pues es oportunista o por conveniencia; son grupos que la escuela determina y
el investigador no tiene injerencia en ello.
Resultados
1. Construcción del evento contextualizado
Para
esta primera etapa del método de trabajo, de acuerdo a la metodología Dipcing,
se analizan los textos más usados en asignaturas de la formación profesional de
los estudiantes. Se ocuparon los libros de texto como Deitel, P. y Deitel, H.
(2012). "Java, cómo programar". Meyer, B. (1998). "Construcción
de software orientado a objetos".
De
acuerdo al proceso de análisis de textos de la fase epistemológica de la MCC,
el análisis se lleva a cabo a través de identificar en qué tipo de conceptos de
la ingeniería se emplea la matemática, cómo los emplean y qué notación les
imprimen (Camarena, 2000, 2001). Se Identifica que, hasta el semestre cursado
por los estudiantes, en sus textos no aparecen los números complejos, por lo
que se procede a determinar la forma en que se puedan vincular estos números
con los conocimientos que tienen sobre tecnología.
Así,
se construye un event-cont robusto
donde la vinculación se establece a través del desarrollo de una calculadora de
números complejos por parte de los alumnos.
En
la teoría de la MCC, se denomina event-cont
robusto a aquel evento que requiere de actividades complejas de
aprendizaje, donde hay más de dos asignaturas presentes para abordar
exitosamente el evento (Camarena, 2001).
De
esta forma, se trata solamente de un event-cont,
no de varios. Luego, se procede a verificar su validez de contenido, de
constructo y de criterio.
1.1. Validez de contenido. Los
números complejos se construyen a partir de los números reales. Lehmann (2015)
comenta que el conjunto de todos los números reales es un subconjunto del
conjunto de los números complejos, los cuales son considerados como pares
ordenados de números reales, es decir, de la forma z=(x,y) o bien z=x+iy, donde i2=-1, además, x, y están en el
conjunto de los reales. Si se toma un número
real "r" cualquiera que sea éste, se puede reescribir como r = r +
(0)i, lo que conduce a expresarlo o verlo como un número complejo, así cada
número real pertenece al conjunto de los números complejos, por lo que se puede
asegurar que el conjunto de los números reales es un subconjunto de los números
complejos.
Las
operaciones de suma, resta, multiplicación, división, potencia de un número
complejo elevado al exponente n y el cálculo de la raíz n-ésima que se realizan
entre números complejos, se efectúan entre los elementos reales x e y
mencionados anteriormente (Lehmann, 2015). Además, al igual que con el campo de
los números reales, en los números complejos, la característica de campo obliga
a que el resultado de las operaciones de suma, resta, multiplicación y división
con dos o más números complejos sea siempre un número complejo (Lehmann, 2015),
(Kreyszig, 2013). Cabe mencionar que estas
operaciones se efectúan de manera similar que en el conjunto de los reales, a
excepción de la división, en donde se introduce la noción de conjugado
(Lehmann, 2015).
Por otra parte, a diferencia de un número real cuya raíz
n-ésima, no siempre existe (Stewart, Redlin y Watson, 2012), la de
un número complejo siempre existe, además da n raíces distintas (Lehmann,
2015). Cabe recalcar que para agilizar el
proceso de hallazgo de la raíz n-ésima de un complejo, es muy importante
representar a dicho número en sus formas trigonométrica y/o exponencial
(Lehmann, 2015).
1.2. Validez de constructo. De acuerdo a
la teoría matemática, la definición formal de un número complejo es una pareja
ordenada de números reales, es decir z=(x, y) con x, y números reales (Lehmann, 2015), como se mencionó
anteriormente.
Para
el caso de las ingenierías, es importante el manejo operativo entre números
complejos (Flores y Camarena, 2012), de esta forma se determina que los
estudiantes deben dominar el manejo operativo entre números complejos.
1.3. Validez de criterio. Para
determinar la validez de criterio se
procedió a entrevistar a profesores expertos de ISC de UPIIZ-IPN en los temas
de las asignaturas que le permiten al estudiante desarrollar la calculadora
para operaciones con números complejos.
Primero, en relación a desarrollar una
calculadora que realice operaciones entre números complejos, se les preguntó: ¿Requieren los estudiantes conocimientos fuertes de números
complejos?, ¿Por qué?
Luego, para que funcione bien la calculadora sobre los números
complejos: ¿Qué tanto necesitan los alumnos entender las operaciones entre
números complejos?
El propósito de estas dos
preguntas es saber si la insuficiencia de conocimiento acerca de los números
complejos es un impedimento fuerte o no para que los alumnos desarrollen
adecuadamente una calculadora que pueda realizar operaciones de estos números y
que funcione eficientemente.
Así, a la primera pregunta, el
experto 1 contestó:
Sí,
debido a que la tarea del desarrollador es tener el conocimiento y estructurar
ese conocimiento para poder cumplir con el objetivo del Software que va a
desarrollar y la calidad de dicho software se basa en la profundidad en que se
conocen o desarrollan los requerimientos"; mientras que el experto 2
relata que: " Sí, porque deben conocer bien lo que requieren que
haga un programa, con esto se tiene una mejor calidad en sus programas y se
tiene un adecuado manejo de posibles errores.
Por lo
tanto, la respuesta a la pregunta 1 es unánime: los estudiantes deben conocer
bien el tema de números complejos para que la calculadora sea eficiente,
situación que permite saber si los estudiantes tienen los conocimientos de los números
complejos, determinando que la calculadora que han construido es eficiente.
Como respuesta a la pregunta dos,
el experto 1 dice: " al ser una calculadora, las operaciones son
sus requerimientos principales"; por su lado el experto 2 argumenta que " como comenté en la respuesta anterior, es
importante conocer bien cómo se realizan las operaciones para que su programa
sea de calidad y funcione bien siempre".
Como lo
sostienen los expertos de la carrera de ISC, para el buen desarrollo de una
calculadora de números complejos y para que ésta realice de manera eficiente la
tarea que se le asigne, es necesario e indispensable que los alumnos que la
desarrollen tengan conocimientos muy claros y fuertes sobre estos números. Además, los expertos comentaron que el
desarrollo de una calculadora de números complejos como event-cont es una tarea que respeta perfectamente el perfil de la
carrera de estudio de un estudiante del cuarto semestre de ISC.
2. Didáctica de la Matemática en Contexto.
Para la segunda etapa del método de trabajo se
aplicaron cada una de las nueve etapas de la estrategia didáctica de la
Matemática en Contexto de la fase didáctica de la teoría de la Matemática en el
Contexto de las Ciencias.
Etapa 1:
Identificar los eventos contextualizados.
Este punto fue abordado en la primera etapa del
método de trabajo, referente a la construcción del event-cont.
Etapa 2:
Plantear a los equipos el event-cont.
Se pidió a los alumnos que formaran equipos de
tres integrantes para realizar la actividad, la cual consiste en el desarrollo,
en cualquier lenguaje de programación, de una calculadora que realice
operaciones de suma, resta, multiplicación y división con dos o más números
complejos, que calcule la n-ésima raíz
de un complejo, que calcule las potencias de un número complejo con un
exponente entero, además, que represente estos números en sus
formas algebraica, trigonométrica, exponencial, etc.
Como la muestra es de 15 alumnos para el grupo
experimental, se formaron cinco equipos denominados E1, E2, E3, E4, E5, de tres
integrantes cado uno.
Etapa 3:
Determinar las variables y las constantes del evento por los equipos.
Las variables en el evento son las diversas
operaciones mencionadas anteriormente que deberá efectuar la calculadora, éstas
deben ser identificadas por los estudiantes.
De hecho, la concepción de la calculadora de
números complejos implica realizar las operaciones de suma, resta,
multiplicación y división de dos o más números complejos, así como las
operaciones de cálculo del módulo y de la raíz n-ésima de complejos, de
potencia de un número complejo al exponente n y de la escritura de estos
números en sus diferentes representaciones (algebraica, trigonométrica y
exponencial). También, esto significa la representación gráfica de éstos en el
plano complejo. Así, cada equipo de alumno que desarrolla esta aplicación
determina de manera implícita las variables definidas por las diferentes
operaciones mencionadas que realiza la calculadora.
Etapa 4:
La inclusión de los temas y conceptos matemáticos necesarios para el desarrollo
del modelo matemático y solución del evento.
Durante dos sesiones de clase, se reforzaron
los conocimientos matemáticos previos necesarios de los alumnos para tomar el
curso de números complejos. Se trabajó sobre las diferentes operaciones (suma,
resta, multiplicación, división y cálculo de la raíz n-ésima) de números
reales, las propiedades que los rigen y determinación del conjunto solución de
una ecuación cuadrática. Todo ello, sirve como base para entender la estructura
y las características de los números complejos.
Etapa 5:
La determinación del modelo matemático por los equipos.
Los alumnos determinaron cómo usar las reglas
de cálculo de las operaciones mencionadas y las diferentes formas de
representación de un número complejo cuando concibieron el proceso (algoritmo)
de desarrollo de su aplicación.
NOTA: El tipo de evento contextualizado
robusto, permite englobar las etapas 6, 7 y 8 de la estrategia didáctica de la
MC.
Etapas 6, 7 y 8:
El hallazgo de la solución matemática del evento por los equipos, la obtención
de la solución requerida por el evento y la interpretación de la solución en
términos del evento por los equipos.
Se vigila que la calculadora de cada grupo de
estudiantes realice bien y eficientemente la tarea que se le asigna, es decir,
todas las operaciones mencionadas anteriormente. Así, con los softwares y los reportes
entregados por los equipos de estudiantes, se pudo constatar el desarrollo de
las diferentes calculadoras, como se observa en las figuras 1 y 2.
Figura 1. La calculadora desarrollada por el equipo E1, la
cual realiza la búsqueda de la raíz cúbica del número complejo z=1-i y gráfica de las diferentes raíces en
el plano complejo XY.
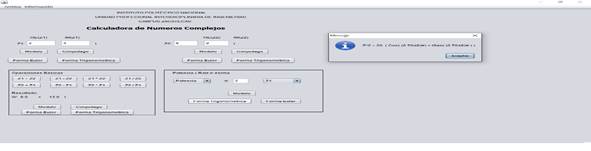
Figura 2. La calculadora desarrollada por el equipo E5,
realiza la potencia del número complejo z=2+4i con exponente dos.
Como se puede ver, los alumnos
presentaron calculadoras con diferentes interfaces; lo que significa que ellos
tienen los conocimientos sólidos en su área de especialidad para realizar una
aplicación. Además, se pudo constatar que la mayoría de las calculadoras
desarrolladas realizan operaciones con un grado de dificultad elevado sobre los
números complejos. Por ejemplo, ellas calculan la raíz de cualquier orden de
números complejos y grafican dichas raíces en el plano complejo XY. Todo ello,
muestra que los estudiantes entienden el concepto de los números complejos y
las diferentes propiedades que los rigen.
Etapa 9:
La presentación de una matemática descontextualizada.
Se retomó la clase sobre los números complejos
para desarrollar la teoría matemática que fundamenta los diferentes conceptos y
operaciones sobre estos números y sus registros de representación.
3. Nivel de aprendizaje
Para
la tercera etapa del método de trabajo se muestra cómo se diseñó el
instrumento, la rúbrica y los resultados.
3.1. Diseño del instrumento
Se diseñó el instrumento del apéndice de
acuerdo a los procesos cognitivos que determinan la construcción del
conocimiento matemático de la tabla 1, propios de la teoría de la MCC.
Según
el ProCog 1, el estudiante debe realizar actividades que conecten los
conocimientos previos con los conocimientos nuevos. Esta situación conduce a
que el estudiante desarrolle actividades con los números complejos
(conocimiento nuevo) donde requiera del conocimiento previo (números reales).
Así,
el estudiante debe poder hacer el tránsito entre registros de representación,
para lo cual el alumno debe pasar de cualquiera de los registros numéricos
algebraico, trigonométrico y exponencial y gráfico, es decir, dado un número
complejo en alguna de sus representaciones, el estudiante debe poder
expresarlos en cualquiera de sus otras representaciones. Para algunas
representaciones de los números complejos, él debe usar las raíces cuadradas en
el conjunto de los números reales, las cuales él necesita para la definición del módulo de los números complejos.
Con
respecto a esto, Lehmann (2015) y Kreyszig
(2013) comentan que si x, y son dos
números reales, entonces la expresión 
es la forma o
representación algebraica de cualquier número complejo, además la
representación polar o trigonomérica de dicho número es 
, donde 
con x ≠0, es
la amplitud o el argumento del número; se observa que cuando x=0 el
número complejo toma la forma de un imaginario puro, de modo que 
si y>0 y 
si y<0; 
es su módulo o valor
absoluto, más aún, su representación
exponencial o forma de Euler es 
, mientras que la representación gráfica del número complejo , se muestra en la figura 3, en donde x es la parte real de
z: Re(z) y la parte imaginaria de z de y=Im(z).
Figura 3. Representación gráfica de un número complejo 
.
De esta forma, para
representar un número complejo en sus formas trigonométrica y exponencial, se
requiere calcular el módulo de este número, lo
que implica el cálculo de la raíz cuadrada de un número real no negativo.
Por
otra parte, se aclara que a diferencia del conjunto de los números reales, el
conjunto de los números complejos no es ordenado. Pues, como se dijo
anteriormente, los números complejos son un conjunto de puntos en el plano
(Figura 3). Éstos no pueden ser odenados
cuando su parte imaginaria no es cero. Entonces, los números complejos pueden
ser comparables siempre y cuando ninguno de estos números a comparar tenga una
parte imaginaria diferente de cero (Kreyszig, 2013).
Por otro lado, Lehmann
(2015) comenta que los módulos de los números complejos
son números reales no negativos, pues son las raíces cuadradas de números
reales, y desde luego éstos, sí, pueden ser ordenados.
Para la identificación de este proceso
cognitivo (ProCog 1) se diseñan actividades que corresponden a un propósito muy
claro de acuerdo a los procesos cognitivos, como se describen en la tabla 2.
Para el ProCog 1, el objetivo es identificar si el alumno sabe que los números complejos no
forman un conjunto ordenado. Aunque son números que se forman a partir de los
números reales que tienen la propiedad de ser números ordenados, los números
complejos no son ordenados (Kreyszig, 2013). Asimismo, el alumno no debe
ordenarlos ya sea que estén en cualquiera de sus representaciones.
Tabla 2. Intención de cada pregunta de la actividad 1, en
relación a los procesos cognitivos (ProCog 1).
|
Pregunta |
Intención de la pregunta |
|
Sean Halle la forma
trigonométrica, de Euler y la representación geométrica de |
Tránsito entre registros de representación de
los números complejos. |
|
De ser posible, ordene los números:
|
Orden de los números complejos definidos por : ü las raíces cuadradas
de un número real negativo. ü la raíz cuadrada de un número racional no negativo. |
|
De ser posible, ordene los
números:
(Argumente su
respuesta). |
Orden de los números complejos definidos en su forma algebraica con partes real y/o
imaginaria |
|
De ser posible, ordene los
números:
|
Orden de los números
complejos definidos en su forma algebraica con sólo la parte imaginaria. |
|
De ser posible, ordene los
números:
|
Orden de los módulos de los números complejos. |
En el ProCog 2, se requiere el
dominio de la operatividad entre números complejos. Es decir, se necesita que
los estudiantes puedan realizar operaciones aritméticas con estos números
complejos. Cabe mencionar que ellos deben poder
realizar las operaciones de suma, resta, multiplicación y división de números
complejos y elevar cualquier número complejo a una potencia entera.
Cada una de estas actividades mencionadas,
requiere la ejecución de operaciones mecánicas. Para
dos números complejos cualesquiera 
Lehmann (2015)
y (Kreyszig, 2013) comentan que las operaciones
de suma, resta multiplicación y división de números complejos, además la
elevación de números complejos a una potencia entera, se definen de las siguientes maneras,
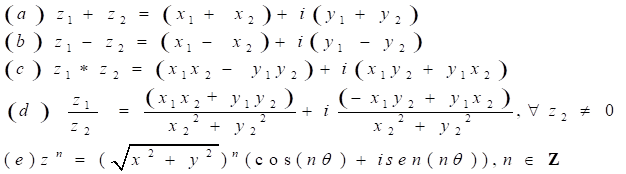
Desde luego, se
necesita hacer operaciones de suma, resta multiplicación, división de números
reales y calcular la raíz cuadrada de números reales.
Para
la identificación de este proceso cognitivo (ProCog 2) se diseñan actividades
que corresponden a los procesos cognitivos 2, como se describen en la tabla 3.
Tabla 3. Intención de cada pregunta de las actividades 2, en
relación a los procesos cognitivos (ProCog 2).
|
Pregunta |
Intención de la pregunta |
|
Sean cuatro números complejos. Calcule |
Sumas o restas de dos números complejos definidos en su
forma algebraica. |
|
Sean cuatro números complejos. Calcule |
Multiplicación de dos números complejos definidos en su
forma algebraica. |
|
Sean cuatro números complejos. Calcule |
División entre dos números complejos definidos en su forma
algebraica. |
|
Sean cuatro números complejos. Calcule |
Calculo de números
complejos elevados a un exponente entero. |
En el ProCog 3, el estudiante debe manejar
procedimientos y técnicas, situación que se refleja en la resolución de
ecuaciones con números complejos.
Determinar
la raíz n-ésima de un número complejo es un proceso que consiste en la búsqueda
de números complejos 
que satisfagan la ecuación 
. Lehmann
(2015) y Kreyszig (2013) indican que para
cualquier complejo, 
, cuya forma exponencial es
, se usa el siguiente procedimiento y técnica 
para hallar las n
distintas raíces n-ésima de este número complejo z.
De manera análoga, para la identificación de
este proceso cognitivo (ProCog 3) se diseñan actividades que corresponden a un
propósito de acuerdo a los procesos cognitivos 3, como se describen en la tabla
4.
Tabla 4. Intención de cada pregunta de la actividad 3, en
relación a los procesos cognitivos (ProCog 3).
|
Pregunta |
Intención de la pregunta |
|
Resuelva |
Determinar el conjunto solución de una ecuación con una
incógnita de grado dos. |
|
Resuelva
|
Búsqueda de la raíz cuarta de un número complejo. |
Cabe recalcar que el ProCog4 hace referencia a
la contextualización del tema matemático de estudio. Por la naturaleza de la
investigación, este proceso cognitivo, solamente lo van a desarrollar los
alumnos del grupo experimental.
3.2. Diseño de la rúbrica de instrumento
Para
el enciso (3), con base en el instrumento, se diseñó una rúbrica (Tabla 5, 6,
7) de acuerdo al grado de dificultad de las actividades, con ésta se analizan
los resultados de cada alumno de los diferentes grupos (experimental y control)
de forma individual.
Tabla 5.
Rúbrica para la actividad 1
|
Asignación de nivel |
|
|
No contesta. |
Nulo |
|
No representa bien el número complejo en ninguna de sus formas. |
Deficiente |
|
No identifica los números como números complejos y los compara. |
|
|
No calcula correctamente ningún de los módulos de los números
complejos y no los compara bien. |
|
|
Representa el número complejo en una sola forma. |
Regular |
|
No identifica los números como números complejos y no los compara. |
|
|
No calcula correctamente ningún de los módulos de los números
complejos, pero los compara bien. |
|
|
Representa el número complejo en dos formas. |
Bueno |
|
Identifica sólo los números como números complejos y no concluye que
no son comparables. |
|
|
Calcula correctamente los módulos de los números complejos, pero no
los compara bien. |
|
|
Representa el número complejo en tres
formas. |
muy bueno |
|
Identifica los números como números
complejos y no los compara. |
|
|
Calcula correctamente los módulos de los
números complejos y los compara bien. |
|
Tabla 6. Rúbrica para la
actividad 2
|
Asignación de nivel |
|
|
No contesta. |
Nulo |
|
No realiza correctamente ninguna de las
tres operaciones de suma y/o resta, o de multiplicación de números complejos,
o de división entre números complejos, o bien de elevación de números complejos a la
potencia entera.
|
deficiente |
|
Realiza correctamente una de tres
operaciones de suma y/o resta; o de multiplicación de números complejos, o
de división entre números complejos, o bien de elevación de números
complejos a la potencia entera.
|
Regular |
|
Realiza correctamente dos de tres
operaciones de suma y/o resta; o de multiplicación de números complejos o de
división entre números complejos, o bien de elevación de números complejos a
la potencia entera. |
Bueno |
|
Realiza correctamente las tres
operaciones de suma y/o resta o de multiplicación de números complejos, o de
división entre números complejos, o bien de elevación de números complejos a
la potencia entera. |
muy bueno |
Tabla 7. Rúbrica para la
actividad 3
|
Asignación de nivel |
|
|
No contesta. |
Nulo |
|
No halla ninguna de las raíces del número complejo. |
deficiente |
|
Halla una de las raíces del número complejo |
Regular |
|
Halla dos de las cuatro raíces del número
complejo. |
|
|
No desarrolla correctamente el proceso de
cálculo de las raíces de los números complejos, pero halla las dos raíces del número complejo. |
Bueno |
|
Halla tres de las cuatro raíces del número
complejo. |
|
|
Desarrolla correctamente el proceso de
cálculo de las raíces de los números complejos y halla las dos raíces del número complejo. |
muy bueno |
|
Halla las cuatro raíces del número complejo. |
|
3.3. Análisis de los
resultados.
Para cada grupo de estudiantes (control y
experimental), con los datos obtenidos de la aplicación del instrumento, se
realiza la distribución de frecuencias de la variable nivel de aprendizaje alcanzado, la cual consta de los niveles "nulo", "deficiente",
"regular", "bueno", "muy bueno" de acuerdo a
la rúbrica.
Para identificar a los estudiantes, se emplea la siguiente
notación: C-n, donde C representa el grupo Control y n es el n-ésimo alumno de
15 estudiantes del grupo Control. De manera análoga, En representa al enésimo
alumno del grupo Experimental.
A continuación, se presentan los porcentajes de
los datos obtenidos de cada grupo de estudio en los diferentes niveles
mencionados, después de la aplicación del instrumento final.
Por la extensión del trabajo, en las diferentes
actividades se seleccionan y analizan sólo algunos resultados de los trabajos
de los alumnos.
Actividad 1
Grupo control
Tabla 8.
Porcentaje de la actividad 1 del grupo control.
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
13.33 |
20 |
20 |
20 |
26.66 |
|
2 |
20 |
46.66 |
0 |
0 |
33.33 |
|
3 |
20 |
46.66 |
0 |
0 |
33.33 |
|
4 |
20 |
46.66 |
0 |
0 |
33.33 |
|
5 |
26.66 |
40 |
13.33 |
6.66 |
13.33 |
Grupo
experimental
Tabla 9.
Porcentaje de la actividad 1 del grupo experimental.
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
13.33 |
6.66 |
20 |
13.33 |
46.66 |
|
2 |
13.33 |
13.33 |
0 |
0 |
73.33 |
|
3 |
13.33 |
20 |
0 |
0 |
66.66 |
|
4 |
13.33 |
20 |
0 |
0 |
66.66 |
|
5 |
13.33 |
20 |
13.33 |
13.33 |
40 |
En
la actividad 1 del instrumento, la pregunta 1 hace referencia a la
representación de los números complejos en sus tres diferentes formas. Para
esta pregunta, se puede observar que en ambos grupos (control y experimental)
sólo 13.33 por ciento de los alumnos no contestó a dicha pregunta.
Además,
el nivel de deficiencia, para la misma pregunta, del grupo control es de 20 por
ciento mientras que el del grupo experimental es solamente 6.66 por ciento;
este resultado indica que la tasa de deficiencia del grupo control es el triple
de la tasa de la deficiencia del grupo experimental.
Además,
20 por ciento de los estudiantes de grupo control tiene un nivel bueno para
esta pregunta contra 13.33 por ciento de los del grupo experimental; sin
embargo, es importante recalcar que esta cantidad de estudiantes, de los grupos
control y experimental, representó correctamente sólo dos de las tres formas
requeridas de los números complejos; esto puede ser que se deba a que la mayor cantidad de los alumnos del grupo
experimental (46.66 por ciento) tiene un nivel muy bueno en la representación
de números complejos, pues, ellos representaron correctamente los números
complejos en las tres formas requeridas.
Por
ejemplo, en la figura 4, se ve que el estudiante C-8 tiene muchas dificultades
para representar los números complejos en alguna de sus tres formas.
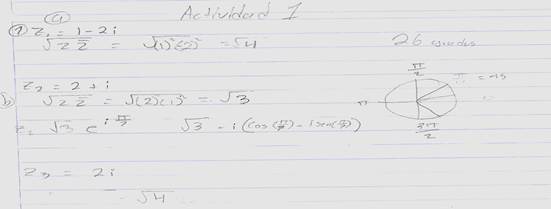
Figura
4. Evidencia del estudiante C-8 del grupo control.
Por su lado, en la figura 5, el alumno E-5
representa correctamente los complejos en sus tres formas requeridas.
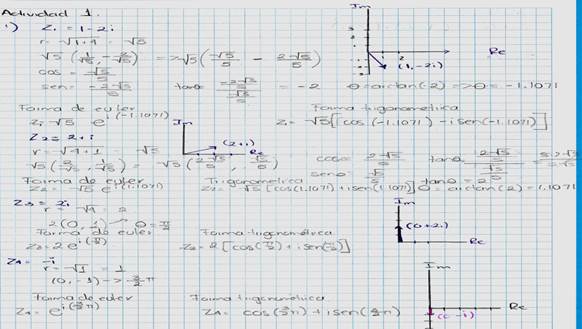
Figura
5: Evidencia del estudiante E-5 del grupo experimental.
Comentarios: Estos
resultados podrían atribuirse a la naturaleza de la misma pregunta, pues se
sabe que los estudiantes del grupo experimental, en el evento contextualizado
(desarrollo de una calculadora de números complejos), construyeron algoritmos
para representar cualquier número complejo en sus diferentes formas, lo cual
podría haberles ayudado a representar los números complejos en sus diferentes
formas durante esta actividad.
Así,
con base en los porcentajes de las tablas 8 y 9, los estudiantes de ambos
grupos (control y experimental) en el nivel muy bueno alcanzan sus porcentajes
mayores, para esta pregunta.
Enseguida,
en la tabla 10, se lista los niveles alcanzados por cada grupo en esta
actividad 1.
Tabla 10. Nivel
de los dos grupos de estudio
|
Pregunta |
Nivel |
|
|
Grupo
control |
Grupo
experimental |
|
|
1 |
Muy bueno |
Muy bueno |
|
2 |
Deficiente |
Muy bueno |
|
3 |
Deficiente |
Muy bueno |
|
4 |
Deficiente |
Muy bueno |
|
5 |
Deficiente |
Muy bueno |
Actividad 2
Grupo control
Tabla 11.
Porcentaje de la actividad 2 del grupo control
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
0 |
6.66 |
0 |
40 |
53.33 |
|
2 |
0 |
26.66 |
6.66 |
40 |
26.66 |
|
3 |
0 |
46.66 |
13.33 |
0 |
40 |
|
4 |
40 |
13.33 |
6.66 |
26.66 |
13.33 |
Grupo
experimental
Tabla 12.
Porcentaje de la actividad 2 del grupo experimental.
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
0 |
0 |
13.33 |
33.33 |
53.33 |
|
2 |
0 |
13.33 |
0 |
33.33 |
53.33 |
|
3 |
0 |
13.33 |
6.66 |
20 |
60 |
|
4 |
33.33 |
13.33 |
6.66 |
20 |
26.66 |
Para
la pregunta dos de la actividad 2, la cual se refiere a la realización de las operaciones
de multiplicación de números complejos, las tablas 11 y 12 indican que 53.33
por ciento de los alumnos del grupo experimental que contestaron con un nivel
muy bueno a ella, mientras el 40 por ciento de los del grupo control
respondieron bien a dicha pregunta. Esto indica un nivel muy bueno para el
grupo experimental y un nivel bueno para el grupo control.
En
la figura 6, se puede observar como el alumno C-3 no efectúa bien el primer
producto de números complejos, pues él se equivoca en el valor de la parte
imaginaria del segundo factor.
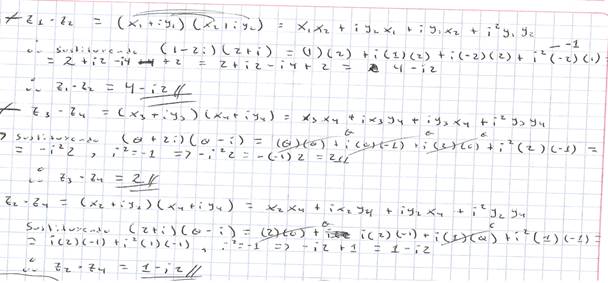
Figura
6. Evidencia del estudiante C-3 del grupo control.
En la figura 7, se observa que el
estudiante E-3 realiza muy bien las tres operaciones de esta pregunta tres.
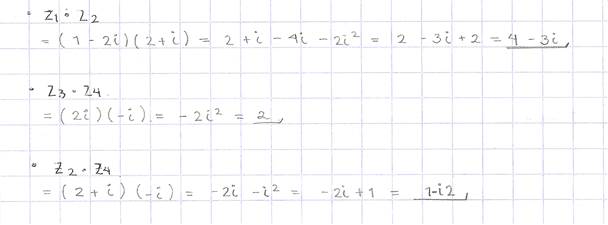
Figura
7. Evidencia del estudiante E-3 del grupo experimental.
Comentarios.
Los resultados del instrumento muestran que la realización de las etapas 3, 4,
5, 6, 7, 8, 9 de la estrategia didáctica de la MCC, podría haber ayudado a los
alumnos del grupo experimental a entender este tema de esta tarea, ya que para
desarrollar
el software (el evento contextualizado), en particular para hallar un algoritmo
para la multiplicación de dos números complejos, los estudiantes tuvieron que
entender el proceso para multiplicar dos números complejos.
Enseguida, la tabla 13 resume los niveles
alcanzados por cada grupo en esta actividad 2.
Tabla
13. Nivel de los dos grupos de estudio.
|
Pregunta |
Nivel |
|
|
Grupo
control |
Grupo
experimental |
|
|
1 |
Muy bueno |
Muy bueno |
|
2 |
Bueno |
Muy bueno |
|
3 |
Deficiente |
Muy bueno |
|
4 |
Nulo |
Nulo |
Actividad 3
Grupo control
Tabla 14.
Porcentaje de la actividad 3 del grupo control.
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
13.33 |
53.33 |
13.33 |
0 |
20 |
|
2 |
20 |
46.66 |
13.33 |
0 |
20 |
Grupo
experimental
Tabla 15. Porcentaje
de la actividad 3 del grupo experimental.
|
Pregunta |
Nulo |
Deficiente |
Regular |
Bueno |
Muy bueno |
|
1 |
13.33 |
33.33 |
13.33 |
0 |
40 |
|
2 |
26.66 |
6.66 |
13.33 |
0 |
53.33 |
Para
la segunda pregunta, donde se busca la raíz cuarta de un complejo, los
resultados de las tablas 14 y 15 fueron casi semejantes a los de la pregunta
uno; pues el grupo experimental contestó con nivel muy bueno a dicha pregunta
(53.33 por ciento), mientras tanto el grupo control mantiene su tasa alta en el
nivel deficiente.
Por
ejemplo, el alumno C-12 (figura 8) tiene dificultades enormes para hallar las
raíces de un número complejo, pues no lo escribe en ninguna de sus formas
adecuadas (trigonométrica y/o exponencial) para la búsqueda de la raíz n-ésima
de un número complejo.
Figura
8. Evidencia del estudiante C-12 del grupo control.
Sin
embargo, el alumno E-13 (figura 9) halla las raíces de un número complejo con
facilidad.
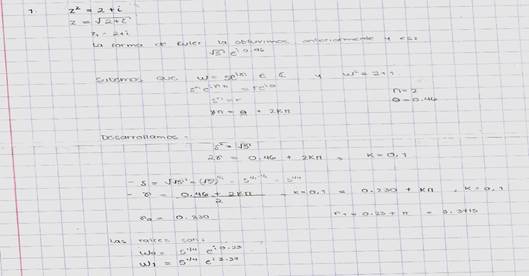
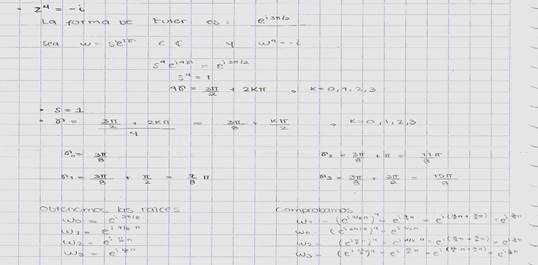
Figura
9. Evidencia del estudiante E-13 del grupo experimental.
Enseguida, la tabla 16 resume los niveles
alcanzados por cada grupo en esta actividad 3.
Tabla
16. Nivel de los dos grupos de estudio.
|
Pregunta |
Nivel |
|
|
Grupo
control |
Grupo
experimental |
|
|
1 |
Deficiente |
Muy
bueno |
|
2 |
Deficiente |
Muy
bueno |
Comentarios
a ambas preguntas. El nivel muy bueno en
estas dos preguntas del grupo experimental sobre el cálculo de las raíces
n-ésimas de un número complejo, contra el nivel deficiente del otro se podría
justificar con el desarrollo de la calculadora de números complejos de los
alumnos del grupo experimental, quienes programaron un algoritmo para hallar
las raíces n-ésimas de cualquier número complejo.
Conclusiones
Para abordar el
objetivo de investigación: determinar cómo
favorece la tecnología con la teoría de la MCC la construcción del conocimiento
de números complejos en los alumnos, se comparó el nivel de conocimiento de los
números complejos de dos grupos de estudio (grupo de control y grupo
experimental), donde el grupo control tomó un curso tradicional de matemáticas y
al grupo experimental se le aplicó la estrategia didáctica de la MC con la tecnología en event-cont.
El event-cont
fue construido como un
evento
robusto, el cual consistió en el desarrollo de una calculadora de números
complejos por parte de los alumnos.
Para
evaluar el nivel de construcción de conocimiento de los números complejos de
cada grupo de estudiantes, se diseñó un instrumento de acuerdo a los cuatro
procesos cognitivos que determinan la construcción del conocimiento matemático,
propios de la teoría de la MCC; este instrumento se aplicó a cada uno de los
alumnos de los dos grupos de manera individual. Además, se diseñó una rúbrica con
la cual se analizaron los resultados de cada alumno de los diferentes grupos
(experimental y control) de forma individual.
Los
resultados de la aplicación de la estrategia didáctica de la MC arrojan que, el
reforzamiento de los conocimientos matemáticos previos necesarios de los
alumnos durante el proceso de enseñanza y aprendizaje fue indispensable; en
particular, sobre los conocimientos previos en los que ellos salieron
deficientes. Con lo anterior, los estudiantes pudieron construir su
conocimiento sobre los números complejos, porque ellos establecieron la
conexión entre el tema de los números complejos y los conocimientos previos,
como lo establece Ausubel con su definición de aprendizajes significativos
(Camarena, 2017).
Además,
el diseño de los algoritmos en equipos de tres integrantes, para el desarrollo
de software, ayudó a los estudiantes a entender el tema de estudio, es decir,
realizar operaciones con complejos y escribir éstos en sus diferentes formas de
representación; con esta situación se favoreció el trabajo en equipo (Camarena,
2017). Más aún, para desarrollar una caculadora
que realice bien y eficientemente la tarea que se le asigna, los estudiantes tuvieron que entender el concepto de
los números complejos y las diferentes propiedades que los rigen. En este
pasaje se identifica cómo pueden pasar de lo concreto a lo abstracto para el
diseño de la calculadora, mostrando parte de la conceptualización de los
números complejos como lo menciona la teoría de la Matemática en el Contexto de
las Ciencias (Camarena, 2017).
Por
otro lado, en las diferentes actividades de este instrumento, gracias a la
realización del event-cont, los
estudiantes del grupo experimental no sólo desarrollaron los cuatro procesos
cognitivos de construcción de conocimientos matemáticos, en particular sobre
los números complejos, sino que mostraron un buen desempeño con respecto a los
del grupo control. Con lo anterior, es importante mencionar que el event-cont motivó a los estudiantes para
que hicieran más ejercicios sobre números complejos e indagaran más sobre el
tema para aprender mejor, situación que con los cursos tradicionales no se
observa.
Como
el objeto de estudio de la carrera de ISC es la tecnología, y los alumnos de
esta ingeniería pueden construir tecnología gracias a los conocimientos
adquiridos en las asignaturas relacionadas a la ciencia de la computación,
entonces, el docente de matemáticas puede aprovechar esta situación para
diseñar e implementar event-cont
relacionados con la tecnología, donde ellos apliquen sus conocimientos, como lo
establece la teoría de la Matemática en el Contexto de las Ciencias.
Agradecimiento: El autor agradece a los dos
árbitros anónimos por las correcciones y comentarios a este artículo.
Referencias
bibliográficas
·
Ausubel, D. P. (1968). Educational
psychology: A cognitive view. Holt, Rinehart and Winston. New York.
·
Brousseau, G. (2002). Teoría de las situaciones didácticas en matemáticas. Edit. Kluwer
Academic Publishers.
·
Brousseau, G. (2008). Ingeniería didáctica y epistemología de la matemática. Países
Bajos: Edit. Pitágoras.
·
Camarena, G. P. (1984). El
currículo de las matemáticas en ingeniería. Memorias de las Mesas redondas
sobre definición de líneas de investigación en el IPN. México.
·
Camarena, G. P. (1990). Especialidad
en docencia de la ingeniería matemática en electrónica. México: Editorial
ESIME-IPN.
·
Camarena, G. P. (2000).
La Matemática en el Contexto de las Ciencias: Modelo Didáctico. Documento
de trabajo de la Red Internacional de Investigación MaCoCiencias. México:
Editorial ESIME-IPN.
·
Camarena, G. P. (2001). Reporte técnico del proyecto de
investigación titulado: Modelos
matemáticos como etapas de la matemática en el contexto de la ingeniería,
Núm. de registro: 2000731-CGPI-IPN. México: Editorial ESIME-IPN.
·
Camarena, G. P. (2002). Metodología
curricular para las ciencias básicas en ingeniería. México: Revista
Innovación Educativa. 2(10), 22-28, primera parte y 2(11),
4-12 segunda parte.
·
Camarena, G. P. (2014). Un
modelo para el diseño de material computacional interactivo. Revista Iberoamericana de Informática
Educativa, Núm. 19, pp. 3-16, de la Asociación para el desarrollo de la
Informática Educativa (ADIE). España.
·
Camarena, G. P. (2015). A
treinta años de la teoría educativa "Matemática en el contexto de las
Ciencias". Innovación
Educativa, ISSN: 1665-2673 vol. 13, número 62.
México.
·
Camarena G. P. (2017). Didáctica
de la Matemática en Contexto. Revista Educação Matemática Pesquisa, Vol. 19, Núm. 2, pp. 1-26, Brasil.
·
Departamento de Gestión
Escolar UPIIZ-IPN (s.f.). SAES. Recuperado de
http://www.zacatecas.ipn.mx/GestionEscolar/Paginas/SAES.aspx
·
Flores, A. I. P. y Camarena, G. P. (2012). La
interdisciplinariedad: nivel superior. En R. D. Gutiérrez, D. C. Ceniceros, y
V. H. Monárrez (Coords.), Procesos de enseñanza y aprendizaje: estudios en el
ámbito de la educación media superior y superior, pp. 150-167.: Redie,
Colección Experiencias de investigación, Durango, México.
·
Kreyszig,
E. (2013). Matemáticas avanzadas para
ingeniería. México: Limusa.
·
Lehmann,
H. (2015). Álgebra. México: Limusa.
·
Ndjatchi, M. K. C. (2018).
La tecnología en eventos contextualizados para la construcción del conocimiento
de números complejos en ingeniería en sistemas computacionales. Tesis de
Doctorado. Centro Universitario Mar de Cortés. México.
·
Ruiz,
M. L. (2014). La transformada de Laplace
en el contexto de los circuitos eléctricos. Tesis de Doctorado en
Educación, Universidad KINO. México.
·
Stewart, J., Redlin, L. y Watson,S.(2012). Precálculo: Matemáticas para el cálculo. Sexta
edición. México: Cengage learning.
Apéndice
Instrumento
de evaluación de los conocimientos de los números complejos.
ACTIVIDAD 1
1) Sean 
cuatro números
complejos.
Halle la forma trigonométrica,
de Euler y la representación geométrica de 
(argumente su
respuesta).
2) De ser posible, ordene los números: 
donde 
es la raíz cuadrada del número a (Argumente su respuesta).
3) De ser posible, ordene los números: 
(Argumente su
respuesta).
4)
De ser posible, ordene los números: 
(Argumente su
respuesta).
5) De ser posible, ordene los números: 
(Argumente su
respuesta)
ACTIVIDAD 2
1) Sean 
cuatro números
complejos.
Calcule 
(Argumente su
respuesta).
2) Sean cuatro números complejos.
Calcule
(Argumente su
respuesta).
3) Sean cuatro números complejos.
Calcule 
(Argumente su respuesta).
4) Sean 
cuatro números complejos.
Calcule
(Argumente su
respuesta).
ACTIVIDAD 3
1)
Resuelva 
, la ecuación 
2) Resuelva , la ecuación 